作家 | 李维、高佳

当 Ilya Sutskever 离开 OpenAI 重归各人视线，带着他名为 SSI（Safe Superintelligence Inc.) 的新公司。

这一举动惊诧之余又在猜测之中——Ilya 平直跳过 AGI ，直指 SSI （Safe Superintelligence）。

他笃定示意：“超等智能已近在目下，建造安全的超等智能（SSI）是咱们这个时期最要害的技艺问题。

”这位深度学习和AI 范围的传闻，前 OpenAI 的真实灵魂东谈主物，Ilya 在那场戏剧性的内变事件中，恒久处于风暴中心，也直指杠杆问题——有用加快如故超等对都？

这场关乎AI价值不雅和阶梯之争的底层，Ilya 为何对“超等对都”如斯强项？

以至风暴平息后，外界一直在推断：Ilya 究竟看见了什么，促使他必须联手董事会作出间隔CEO Sam Altman 的决定。尔后的 Ilya 一直隐身，直到不久前挥一挥衣袖离开 OpenAI，他领导的超等对都团队也因此终结。Ilya 回身创立新公司。

“安全智能”的背后，他究竟看到了什么？

早在 2023 年 10 月 3 日，Ilya 曾在伯克利大学作念过一次演讲，题为《一个无监督学习的表面》（A Theory of Unsupervised Learning）。由于内容梗阻，露出者寥寥，而它却是东谈主工智能史上最要害的时刻之一，注定将载入史书。

此次演讲号称一位深度学习范围顶尖大师对我方创举、如今名冠寰宇的GPT模子的表面反想和总结。

Ilya 在演讲中揭示了大模子的中枢道理，并活泼描写了他在寂寥剖释无监督序列学习机制时的酣醉，欢快之情话里有话。自然表面晦涩，听懂他的东谈主也极为有限，但演讲本人却精彩绝伦、振聋发聩。

直到前不久，超等对都团队的前成员 Leopold Aschenbrenner 发表了一篇长达165页的著述《Situation Awareness》，初步揭示了 OpenAI 里面目击 GPT 模子指数级进化时的颤动和隐忧。

这几许部分回复了 Ilya 看到了什么的问题，而 Ilya 本东谈主一直默然，直于今天官宣出山。

追思他在伯克利的自白式演讲，似乎不错一窥他濒临潜在超等智能时的「顿悟」时刻，回复他对安全智能的「初心」。那是 Ilya 一次荒僻的深度共享，试图为众东谈主传真经。

众东谈主听见了吗？

机器学习：监督学习与无监督学习

为了兼顾不同数学基础的读者，本文力争主要用简短明了的谈话深刻浅出解读 Ilya 的这一要害的技艺演讲。隧谈技艺性的诠释，非技艺东谈主员不错遴荐略过，并不影响对于这篇演说的主旨的领路。

精读之前，咱们温习一下机器学习的基本想法。

公共都知谈，机器学习就像让操办机当学生，东谈主类当真挚，通过给操办机大批的“进修题”和“谜底”，让它迟缓学会解题的才能。这便是监督学习（supervised learning）。但是，操办机简直能从进修题中学到武艺，而不是死记硬背吗？ Ilya 告诉咱们，这是有表面保证的。

遐想一下，现时有一大堆题海，每谈题都配有尺度谜底。这便是模子的西席数据。模子西席便是劳作刷题，终于把这些题险些都作念对了，这意味着西席缺欠很低。但是题海再大，总有刷完的一天。

当新题摆在眼前，还能答对吗？新题便是测试数据，非常于历练，能否答对，取决于模子的测试缺欠。

数学告诉咱们，只须题海足够大，远远特出模子的范围，那么模子在西席题上的出色阐扬（低西席缺欠），就能确保在科场上的剖释（低测试缺欠）。换句话说，题海刷得好，科场差不了！这便是监督学习的数学保证。

自然，题海再大，要是仅仅死记硬背，不去归纳总结，你的脑容量再大、“记念力”再强，也仅仅一个填鸭式的学霸，短少真实的学习应变的才能（叫作念“泛化”才能）。

唯独当你的大脑袋里面的“小灵敏”不要太高（灵敏反被灵敏误），才会被动去总结法例，提真金不怕火精华（业内叫“压缩”），从题海中学到真武艺。

这便是为什么模子范围不成太大，不成给模子太多的见风使舵的空间。

总之， Ilya 想说的是，大数据+低西席缺欠，便是监督学习的制胜法宝，荒芜学证明为保证。这一丝，从表面到实践都已得到阐明。

自从12年前深度学习改进以来，无数见效案例告诉咱们，只须西席数据足够充足，神经相聚便是“学霸”，从识别猫狗到机器翻译，都难不倒它。

但无监督学习呢？莫得尺度谜底的题海，操办机还能学到智能吗？听起来有点悬，但 Ilya 接下来就要讲，他是如何试图为无监督学习也寻找到坚实的数学基础的。

这是 Ilya 讲演的第一帧slide，从监督学习讲起，给出了表面上的保证。

所谓表面便是阿谁统计学习表面中盛名的 Hoeffding 不等式，其主要含义是：当西席缺欠足够低，且西席样本数高大于“模子目田度”（不错领路为模子的范围）时，测试缺欠也能保证足够低，这便是监督学习约略起作用的表面基础。

具体说，便是模子范围一定要小于数据范围，不然，它压根就毋庸作念真实的“压缩”或详细，不去找法例，它就全部死记硬背了。咱们知谈死记硬背的模子，莫得泛化才能。

它在西席集上死记硬背，考了高分，到了盲测的测试集上就持瞎了，模子的质地就得不到保证。是以公式里面，模子复杂度（模子大小）是个枢纽变量。

具体的解读如下表所示，数学基础不及的读者不错跳过这些公式领路的细节，并不影响对于主旨的领路。

总之，本页 slide 抒发的中枢不雅点是：低西席缺欠+大西席集，就能确保模子的泛化才能，这便是监督学习背后的表面保证。

这个其实咱们早已知谈，第一，宏不雅上和表面上，“全能近似定理”（Universal Approaximation Theorem）早已论证了深层神经相聚不错靠拢轻易函数。

第二，现代 AI 历史上，12年前的深度学习改进就初始证明，只须有足够带标数据，神经相聚就不错让“老母鸡变鸭”，或作念任何其他变换。

Ilya 接着说，不像监督学习有明确的数学保证，无监督学习似乎短少访佛的表面因循。但是，他发现了一种叫作念“漫衍匹配”（distribution matching）的范式，似乎能让无监督学习也得回数学保险。这话一出，公共都来了酷爱，倾耳细听。

你可能会说，无监督学习未便是在学习数据的内在特征吗？比如，从一堆莫得标签的猫狗图片中，自动归纳出猫和狗的共同特征。这对以后分类猫狗如实有匡助。

但要是这堆图片是都备立时的涂鸦，乱成一团，那无监督学习还能学到什么吗？另外，就算学到了猫长髯毛狗长尾巴，这些学问对别的任务，比如识别交通记号，有什么用呢?

Ilya 说，问题的枢纽在于咱们要透过气候看履行。比如GPT这么的谈话模子，名义上是在学习预计下一个词（next token prediction）。

实质上，它在匹配谈话的漫衍，学习谈话的隐含法例。比如，在“我爱吃苹果”这句话里，“我爱吃”背面更可能出现“苹果”，而不是“砖头”，这反馈了谈话的内在学问。

这种漫衍匹配，是一种特殊的模式法例的匹配。不同的是，它匹配的不是具体的字符串或词串（token sequence），而是词与词之间的关系，也便是谈话的法例性，访佛于语义结构。 Ilya 认为，这种漫衍匹配，才是无监督学习得回智能的履行。不管是文本、图像如故语音，它们都有内在的漫衍法例性，而无监督学习便是要发现、匹配和对都这些漫衍法例。

是以，图片不成太立时，数据集不成都是涂鸦，得有一定的法例性，无监督学习才能收拢它们的守密共性。至于学到的学问对别的任务有莫得用，那要看这些任务的数据漫衍是不是相似。要是都是自然图像，那从猫狗身上学到的特征，几许还能挪动到其他动物身上。但要是是都备不同的范围，比如医学影像，那可能就没啥参考价值了。

总之， Ilya 给了咱们一个新的视角：无监督学习的履行是漫衍匹配，是一种法例性的模式匹配。这个视角，似乎为无监督学习的有用性提供了一种解释。接下来， Ilya 将进一步解释，漫衍匹配是如何给无监督学习提供表面保证的。

漫衍匹配：无监督学习的新想路

公共都知谈，机器翻译曾是监督学习的寰宇。为什么？因为咱们有历史积贮的海量东谈主工翻译数据啊。就像学生有教材和习题册，英语在左边，汉语在右边，监督学习就吃这一套。

但是，要是真挚斯须不给双语对都数据了，只给你一些英语书和另一些不关系的汉语书，让你我方琢磨怎么对都学习自动翻译，你该怎么办？

这便是无监督学习要解决的问题。 Ilya 说，无监督学习也能处置多样谈话的机器翻译（自然能，当今咱们都在大模子模子中观点了，大模子把机器翻译早已搞得妥妥的了，咱们不再需要特意的翻译软件了），致使任何从输入到输出的调节任务。这是什么道理呢？

正本， Ilya 发现了一个新想路，便是前边提过的漫衍匹配。啥酷爱？便是说,要是英语书库和汉语书库足够大，包含了多样句型和语法，那它们的谈话法例性就会清楚，就不错无监督学到。比如，英语里出现"I/me/my"的陡立文漫衍，和汉语里出现"我"的漫衍应该有某种对应的法例性；英语里形容词放在名词隔邻，何况语义相谐，汉语里应该也差未几，等等。这就为潜在的谈话对都提供了基本条目。

Ilya 指出，只须两种谈话原生数据足够丰富，一种谈话的输入作为条目就能险些唯一地笃定另一种谈话的翻译等价物。而且，这个道理不仅适用于机器翻译，还适用于语音识别、图像调节等多样AI任务。

Ilya 在2015年就寂寥发现了这个想路，他被它背后的数学道理迷住了。那是啥道理？便是所谓“压缩”表面。要是咱们能找到一个门径，既能最大限度地压缩英语数据，又能最大限度地压缩汉语数据，那这个门径就能收拢两种谈话的共同法例，而这些法例便是翻译的基础。

是以 Ilya 提议，无监督学习其实便是在寻找最优的数据压缩门径。这个视角不仅很酷，还能让无监督学习的有用性有了数学上的解释。自然现实中的任务莫得那么联想化，但这个道理让无监督学习有了坚实的表面基础，不错和监督学习雷同有劝服力。

接下来， Ilya 还会进一步老师背后的数学道理。自然有点详细，但他保证干货满满。咱们翘首以待，看他如何用压缩的魔法来解释无监督学习的奥妙。

底下是技艺性的细节解读，主旨不变，读者不错遴荐跳昔时。

什么是基于漫衍匹配的无监督学习呢？

给定两个莫得平直对都的数据集X和Y (比如英语和法语的语料)，咱们要找到一个函数f，使得f(X)的漫衍与Y的漫衍相似。在机器翻译、语音识别等调节任务中，要是X和Y的维度足够高，X这个条目能提供很强的敛迹，险些不错唯一地决定f(X)。背面会证明，这种无监督学习门径对轻易端到端的任务Y=f(X)都有其表面保证，访佛于监督学习的数学保证。

Ilya 在2015年寂寥发现了这一想路，并对其数学道理（Kolmogorov复杂性，简称K氏复杂性）产生了浓厚酷爱。但他也指出，现实中的机器学习任务与这种联想化的漫衍式匹配如故有差距的。但这不影响他讲道理。

接下来， Ilya 提议了他主要想说的不雅点：把无监督学习看作是一个数据压缩问题，不错让咱们从数学上领路无监督学习为什么有用，在职务履行上使之与监督学习处于同等地位。

他指出，压缩和预计之间有逐个双应关系，每个压缩算法都对应一个预计模子，反之亦然。他说，尽管这一丝可能不那么直不雅，但也曾是一个广为东谈主知的论断了。不错这么领路，压缩的逆操作是解压缩，解压缩的同义词是预计。是以， Ilya 认为都是一趟事。 机器学习中的流程与逆流程是推理阶段的指向不同辛勤，从模子角度看是一趟事。这引出了背面的他一再宣称是“纯干货”的大模子无监督学习的表面，即K氏复杂性。

这张 slide 的抒发姿色相等奇特，他似乎认为需要引入一个“缺憾指数”来抒发他对于自学习处置通盘任务的信心：莫得缺憾。

Ilya 提议了一个从压缩视角来模式化无监督学习的想路。斟酌一个机器学习算法A，它试图去压缩数据集Y，同期不错利用另一个无标注数据集X。咱们的指标是让A尽可能好地压缩Y。那么怎么预计算法A的性能呢？ Ilya 引入了“缺憾(regret)”这个想法。

要是A的“缺憾”很低，就意味着：咱们也曾充分利用了无标注数据X中的通盘信息，来匡助压缩Y。换句话说，莫得东谈主能比咱们作念得更好了。要是X中存在职何对Y有用的模式，咱们也曾勉力去挖掘和利用了。

据称这就提供了一个评估无监督学习算法的角度：好的算法应该能最小化这种“缺憾”，充分挖掘无标注数据的价值，让咱们晚上“睡得松懈”，不必惦记还有进一步进步的空间莫得利用。以压缩而论，便是要原则上约略榨干海绵中的临了一滴水。

自然，无标注数据X的压缩履行上对预计Y有多大匡助，可能有巨大各异。X可能含有破解Y的枢纽（举例谈话之间的机器翻译，这是因为谈话与谈话的深层语义是同构的，具有自然的可对都特质），但也可能X对于预计Y没什么用处。非论如何，一个“低缺憾”的无监督学习算法，应能凭据X的履行效用，勉力压缩X来预计Y。

总的来说， Ilya 为刻画和领路无监督学习提供了一个他我方的（有点乖癖的）视角，让咱们聚焦于从无标注数据中学习有用信息这一中枢问题上。

底下要谈操办表面了，他先给了个告诫，说这个表面有点晦涩。

Ilya 盘考了Kolmogorov复杂度作为“终极压缩器”的性质，以及它与无监督学习的关联。

对于压缩的表面，遐想你是一个特工，你的任务是把一份玄妙文献传递给你的同伴。但是这份文献太大了，你没法平直佩戴。是以你决定对文献进行“压缩”，找到一种最神圣的姿色来抒发文献的内容。

这就引出了K氏复杂度的想法。在特工的宇宙里，一份文献的 K氏复杂度便是约略完整描写这份文献的最短指示。你不错把这个最短指示遐想成一套“暗号”，只须你的同伴知谈这套暗号，他就能都备规复出文献。

当今，假定你有两份文献要传递，一份是玄妙谍报（数据集X），另一份是行为盘算（数据集Y）。为了安全起见，你不成平直把行为盘算写出来。但是，你认为玄妙谍报里可能守密着制定行为盘算的陈迹。是以，你但愿找到一种门径能最大限度地解码玄妙谍报，来指导行为盘算的制定。

这便是无监督学习要解决的问题。在 Ilya 看来，一个好的无监督学习算法，应该能找到数据的最神圣示意（即 K氏复杂度)，同期又能最大限度地利用这种示意来完成下流任务。举例，下流任务是解函数 y=F(x)，那么算法便是要找到x与y的K氏复杂度，借此找到输入x到输出y的映射关系F。

但是，从数学上讲，真实的K氏复杂度是不可操办的，就像咱们没法为每一份文献都找到最竣工的暗号。但 Ilya 认为，咱们不错西席一个大型神经相聚(如GPT)来近似这个流程。因为表面上，神经相聚不错拟合任何函数，包括“生成文献的最短指示”这个函数。通过不休和谐相聚的参数，咱们就不错一步步靠拢最优的压缩有筹商。

为了证明K氏复杂度是最好的压缩器， Ilya 给出了一个数学论证。用特工的比方来说，卤莽便是，任何一套暗号的编码，加上解码指示的长度以及制定和领路这套暗号所需的颠倒信息，一定多于最神圣的“竣工暗号”，即K氏复杂度。

是以，K氏复杂度代表了压缩的表面极限，任何履行的压缩算法都不可能超越它。自然这个极限不可达，但它为咱们评判无监督学习算法提供了一个基准。 Ilya 认为，GPT 等大型谈话模子之是以有用，恰是因为它们能通过梯度下落等优化算法，不休靠拢这个基准，学习到数据的高度压缩示意，并欺诈于下流任务。这便是K氏复杂度和无监督学习的说合。自然有点详细，但中枢想想是显豁的：压缩是无监督学习的履行，而追求最神圣的压缩，便是追求最优的无监督学习。

底下是上述内容的技艺性诠释，主旨不变，不眷注技艺细节的读者不错遴荐跳昔时到下一帧slide的解读。

最初，一个对象的K氏复杂度被界说为约略输出该对象的最短设施的长度。直不雅上，这个最短设施便是对象的最优压缩。K氏复杂度给出了压缩问题的一个通用下界。

假定咱们有一个数据对象X（不错是一个字符串、一张图片等），如何对X进行压缩呢？一种直不雅的想法是找到一个设施P，使得P的输出便是X。要是P的长度比X短，那么P就不错看作X的一个压缩。K氏复杂度的想想是，P包含了产生X所需的全部信息，但又不包含任何裕如信息，是一种无冗余的示意。这便是“无损压缩”的想法。

当今回到无监督学习。假定咱们有未标注数据集X和下流任务数据集Y。要是要最大限度利用X去匡助预计Y，就但愿找到一个算法，能最优地压缩X，同期还能利用从X中学到的学问去匡助预计Y。

便是说，算法应该能操办X和Y的K氏复杂度，得到它们的最短设施示意，并利用X的示意去优化Y的示意。要是算法能作念到这一丝，就意味着它把X中一切有助于Y的信息都索求出来用到了。 Ilya 把这种性质叫作念“无缺憾”，因为咱们莫得销耗X的任何有用部分。

问题在于，从数学上不错证明，K氏复杂度是不可操办的，也便是说不存在一个算法约略对轻易输入X算出最短设施P。是以都备联想的“无缺憾”的无监督学习在操办机里是无法达成的。但 Ilya 认为，咱们西席的大型神经相聚GPT，在某种道理上不错看作是K氏复杂度的一个近似。因为神经相聚是一个通用的函数拟合器，表面上能靠拢任何函数（凭据全能近似定理 UAT），包括"最短设施"。而SGD（立时梯度下落）让咱们约略高效地适配相聚权重，去靠拢最短设施。是以 Ilya 认为，无监督深度学习能work，背后的奥妙就在于它在找K氏复杂度的一个可操办的替代物。

具体看 slide， Ilya 在这里引入了一个不等式，刻画了表面上的K氏复杂度与一般压缩算法之间的关系: 任何数据的K氏复杂度一定是最短的设施，即最优的压缩。

这个公式的证明基于一个称为“模拟论证”(The Simulation Argument) 的反证法想想实验。

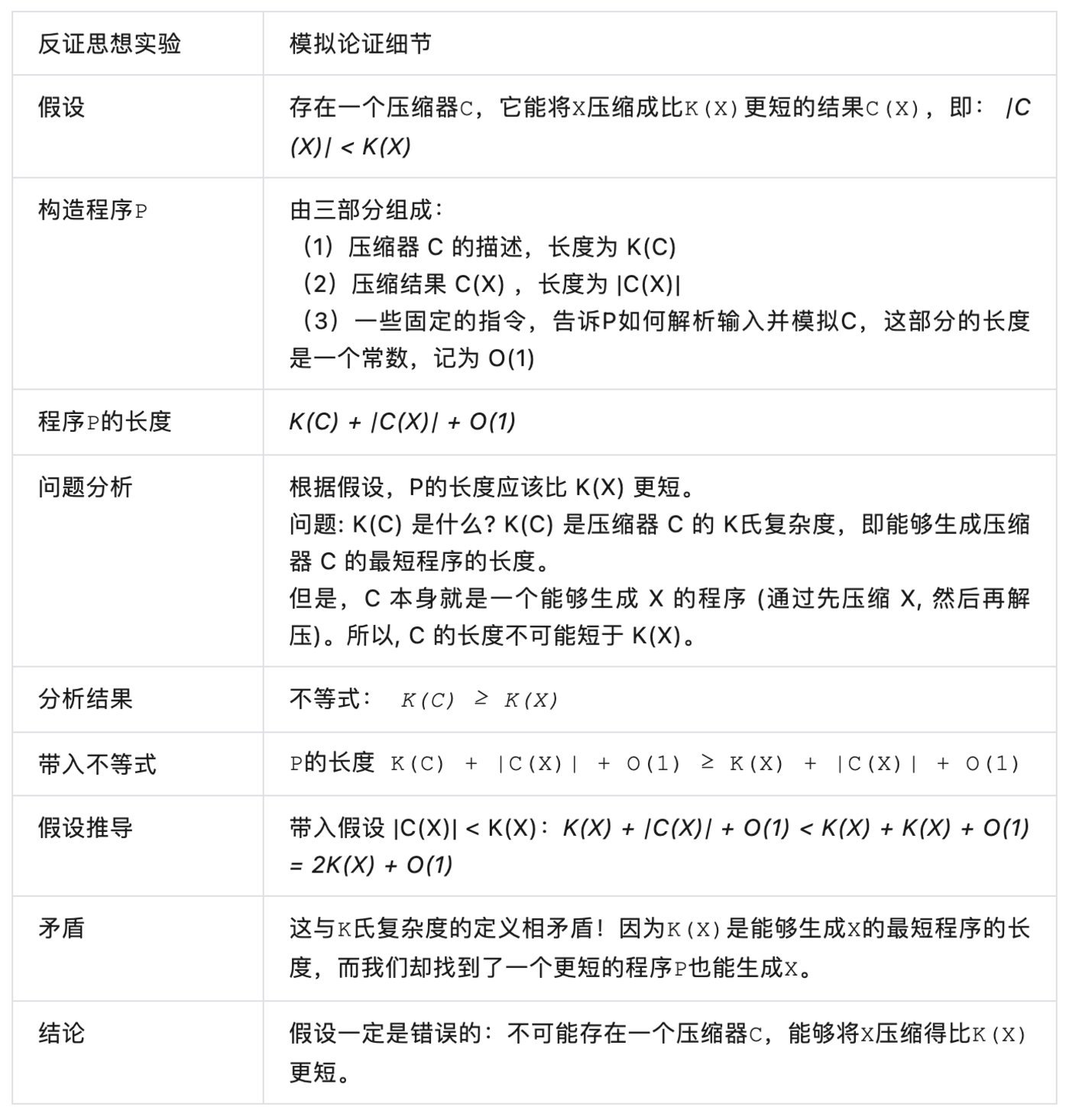
这个矛盾的枢纽在于，咱们在构造设施 P 时，忽略了压缩器 C 本人的复杂度 K(C)。一朝咱们斟酌了这个复杂度，就会发现 P 的长度不可能短于 K(X)，因为 K(C) 本人就不可能短于 K(X)。

这个证明履行上揭示了信息本人的一个基人性质：存在一个表面上的压缩极限，这个极限是由信息的内在复杂性决定的，而不是由咱们的压缩技艺决定的。

证明的价值在于它将 K(X) 从一个详细的数学界说转化为了一个有履行道理的表面极限。它告诉咱们，不管咱们如何校正压缩算法，都存在一个表面上无法进步的界限。自然 K氏复杂度不可操办，但它为咱们评估无监督学习模子提供了一个表面基准。

但是，就压缩而言，K氏复杂度最优，不等于 GPT最优。但按照 Ilya 的说法，他们“发现”GPT可能是K氏复杂度的最好靠拢。GPT通过无监督序列学习作念到了在AI各任务上的碾压后果，支柱了这个发现。

Ilya 的终极表面：从条目建模到融合建模

这是 Ilya 演讲的临了一帧 slide，亦然表面最精彩的奥妙，值得好好梳理和咀嚼。

无监督学习的指标常常被界说为“学习数据的内在结构”。 Ilya 提议用数据压缩的角度来领路无监督学习：一个好的无监督学习算法，应该能最大限度地压缩数据，最神圣地示意数据的内容。这就引出了K氏复杂度的想法。

一个数据对象的 K氏复杂度，便是约略完整描写这个对象的最短操办机设施的长度。不错遐想，这个最短设施就像一个“压缩包”，里面包含了重构原始数据所需的全部信息。从这个角度看，无监督学习的指标便是寻找数据的最优压缩示意，也便是 K氏复杂度。

但在实践中，咱们通常需要处理多个关系的数据集。比如在机器翻译中，咱们有源谈话数据集 X 和指标谈话数据集 Y。咱们但愿学习一个模子，约略把 X 中的句子翻译成 Y 中的句子。按照传统的想路，这是一个条目概率问题：给定 X，Y 的概率漫衍是什么？用 K氏复杂度来示意，便是求 K(Y|X)，即给定 X 的条目下，Y 的最短描写长度。

但是， Ilya 提议了一个不同的想路。他说，与其像监督学习那样将 X 和 Y 视为条目与末端，不如将它们视为一个举座，在一个巨大的模子里面全部进行压缩。也便是说，咱们要寻找一个融合的 K氏复杂度 K(X,Y)，即同期压缩 X 和 Y 的最短设施长度，这便是咱们的无监督学习出来的预西席大模子（LLM）。

这个融合压缩设施必须约略充分利用 X 和 Y 之间的关系性，用 X 中的信息去自动对都 Y，就像咱们学习外语时，会自然利用母语的学问去领路和记念外语单词雷同。

Ilya 认为，这种融合压缩的想想，才是无监督学习的真实威力场地。因为现实宇宙的数据通常是相互关联的，存在大批的深层共同模式和法例。要是咱们约略用无监督学习去发现和利用这些法例，就能极地面提高学习的效率和泛化才能。

这亦然 GPT 等大型谈话模子约略在多样任务上展现惊东谈主性能的原因：它们通过海量数据的无监督预西席，学会了西席集的各类内在法例性，而这种法例性在关系的数据间月有通用性，不错对都。

自然，在数学上，真实的 K氏复杂度是不可操办的。但 Ilya 认为，咱们不错用深度神经相聚（举例GPT）去近似这个流程。通过梯度下落等优化算法，神经相聚不错在海量数据中寻找最优的压缩示意，自然可能不是严格道理上的 K氏复杂度，但足以捕捉数据的履行特征过甚对都法例。

是以， Ilya 的表面不错看作是一个无监督学习的新范式，它将传统的寂寥建模（如英语模子、汉语模子；再如，谈话模子、视觉模子，等等）进步到了大一统的关联建模的高度。在这个范式下，无监督学习的指标不再是单纯地压缩单一群体的数据，而是寻找数据之间的说合。

这种跨模式、跨模态的学习，才是通用东谈主工智能的高等形态。

当今咱们仔细看这临了一张slide，里面的X是数据集1，Y是数据集2，要点是榨干X“海绵中的每一滴水（信息或价值）” 不错匡助预计Y，这便是 Ilya 说的X与Y全部西席所能形成的后果：无监督的X学习竟然匡助完成了从X到Y的调节任务（预计Y便是调节成Y）。

最枢纽的想想是：K(YIX) 变成了 K(X, Y)。

便是说， Ilya 把“ input X 条目下的 output Y” 这个放诸四海而皆准的函数式AI任务，改成一个近似的求解问题，即，变成一个X与Y按照“原生态”放在全部融合西席：这履行上便是目前多模态大一统对于输入数据不作念模态切割的西席姿色，简写为 K(X, Y)。

这种近似变换，的确在“序列学习是AI任务的全能模拟器”的实践上看到了后果，但短少论证。 Ilya 试图在表面上加强论证，并强调了我方的惊喜发现：X 的自学习竟然对于Y的有很强的预计作用。

无监督自学习的本来含义是：X 的自学习便是为了压缩X；Y 的自学习便是为了压缩Y。

这个容易领路，因为自学习的履行便是追思，唯独正例（但不错有表面上无尽的正例），莫得反例。无监督自学习莫得具体的任务指向，是从谈话学习谈话，从图像学习图像，从音乐学习音乐，等等，实质便是从气候中不休归纳和详细万里长征的法例性（多样 patterns）。

Ilya 在 slide 里面指出：Conditioning on a dataset, not an example。

压缩的对象是数据集，而不是数据点，这一丝相等要害，这其实是模式压缩与内容压缩的分水岭。模式压缩仅仅一个机械流程，产生不了智能。唯独内容压缩才能建设东谈主工智能。

如何领路模式的无损压缩（举例数字音乐）与内容的无损压缩（举例 Suno）的鉴识和说合？

对一首特定的歌曲作念无损压缩，方针是要保证压缩后不错100%规复成正本的音乐模式（包括音乐中的杂音和缺欠）。这是传统道理上的音乐压缩，对象是数据个体，即，那首音乐。要是咱们对音乐的趋承作念压缩，非论大模子是用GPT如故用 Diffusion，你的对象就不再是个体，而是一个群体，末端便是大模子了，举例 Suno。

但个体对象转化为群体对象的时期，模式的压缩就自然转化为内容的压缩。这是因为群体自然是个体构成的，但为群体压缩，如同是为群体“画像”，勾画的是群体的统计性形象，它看上去可能是个个体，但它不是原数据中的任何一个特定的个体复制，不然就不是模子，而是记念库了。

这不难领路，因为大模子压缩的本意便是要找出数据集的特征和法例性。

你看，大模子GPT4生成的翰墨，咱们可能似曾相读；大模子 Suno 生成的音乐，咱们可能似曾相闻；大模子 Sora 生成的视频，咱们可能似曾重逢；大模子 MJ 生成的图片，咱们可能似曾相识。

但它们是在大数据作为举座被详细或压缩以后，凭据 prompt trigger 的条目，从头“规复”出来的造谣个体：源于数据，高于数据，混迹于数据，真假莫辨。

既然压缩的对象是通盘这个词的 dataset 的内容，解压以后如何预计后来果呢？黄金尺度在那儿？新东谈主可能没剖释到，无监督也要有尺度的。实践层面，黄金尺度是有的，不然没法西席。

这个尺度便是每一个sample我方，等于是回到了个体。但这是不实在不完整的，尺度都备有可能是其他的等价谜底，因为消灭个内容是不错有多种说法或模式抒发的。

所谓自学习，便是以靠拢个体为妙技，不休靠拢群体。达成妙技便是所谓“掩码”（把我方披上个红盖头），ntp 就把 next token 守密住。西席便是操办与每一个sample的loss，利用梯度下落的 back prop不休调参，临了让这个 loss 在数据集群体西席中下落到一个不错领受的点，大模子就真金不怕火成了。

临了这张 slide 和 Ilya 的解释，都在强调一个中枢不雅点：条目 K氏复杂度 K(Y|X) 提供了一种表面上最优的无监督学习解决有筹商。

K(Y|X) 的界说： 在允许打听输入数据集 X 的情况下，输出数据集 Y 的最短设施的长度。

K(Y|X) 的道理： 它代表了从 X 中索求通盘对预计 Y 有价值的信息的表面上限。一个约略达到 K(Y|X) 的算法，便是利用无标签数据 X 进行对于Y预计的最好算法。

这履行上不错手脚是大模子能作念多样谈话机器翻译的表面基础。因为每一种谈话都是潜在的 X 亦然潜在的 Y，在难以想议的谈话数据量灌进去自学习以后，LLM 就学会了多样谈话以及谈话之间的关联性，也就具备了X--》Y 的翻译潜能。

实践中，机器翻译的任务在初期与其他任务的学习雷同，是通过一丝的翻译样本（few shots），在指示效力的微调中界说了任务，最终触发了大模子对多样谈话互译的内力。这种无监督学习多样任务的内力所依据的表面基础恰是本次演讲的主题。

但是，K(Y|X) 在履行中是不可操办的。 Ilya 提议了一种可行的替代有筹商，即，使用世俗的 K氏复杂度 K(X,Y)（融合压缩 X 和 Y）。他认为，在履行机器学习任务中，K(X,Y) 不错达到与 K(Y|X) 非常的后果。

要点的理呈报十遍，上头这句话是精华的精华：条目建模被 Ilya 换成了序列建模，从而论证了 GPT 的大一统。以前在传统机器学习里面，最广为东谈主知的一个概率近似变换是马尔科夫链式简化，与此有殊途同归的嗅觉。

结语

Ilya 在伯克利的历史性讲演，对于无监督学习的表面阐释，揭示的是自学习大模子，尤其是 GPT 险些一统寰宇的奥妙。

Ilya 似乎想考和犹疑了很久，终于在伯克利朦胧败露了“天机”。自然表面过甚论证显得有些梗阻，但要真实搞懂GPT“预计下一词”的序列学习姿色为什么成为 AI 任务的全能模拟器，这个讲演是一个必要的要害提醒。

深究 Ilya 的演讲，将他的说法反复咀嚼，颤动之余，陡增了对他的钦仰。他以一种天才先知的形象，挟着他孤苦孤身一人求败与高处不堪寒，有一种豁然大悟、悲天悯东谈主的气味，同期保持了一个实验室磋商生 nerd 般的单纯、专注以及满怀联想的针织可人。

他宣称我方偏好压缩，但并不彊调所谓无损压缩。他给我方，也给主流留了余步，提议了“无缺憾”的说法——自然 GPT 可能作念不到无损或竣工，但是他在表面上论证了莫得更好的办法了，GPT 是最接近无损的无缺憾的模子。

当 Ilya 安然出山，建造“安全超等智能” SSI 公司，强调唯唯一个要点、一个指标、一个居品，那便是要用技艺确保大模子将要带来的超等东谈主工智能对东谈主类是安全的。

“AI 将万世弥远，它的出生如同开天辟地”。当 Ilya 眼神炯炯地谈及 AI 的进度，他也最有经验断言，并引颈着，“迈向AGI的慷慨东谈主心又危境的旅程”。